2019年3月5日(火)、2019年度(平成31年度)北海道公立高校入試が実施されました。
裁量問題数学の解説を作成しましたので、アップしておきます。
急ぎで作成したので、誤字・脱字などがありましたら、コメントからソッと教えてください…!
実際の入試問題はコチラから。
[card url=”https://www.hokkaido-np.co.jp/tags/n_examination”]
昨年、2018年度(平成30年度)の数学解説はコチラから。
[kanren postid=”3200″]
どんな入試だった?
近年、稀に見る易しい出題でした。
基礎・基本をおさえ、オーソドックスな解法を覚えておけば解ける問題ばかりで、「裁量問題」といえるレベルではありません。そのため、数学が得意な人にとってはライバルと差をつけにくく、厳しい入試となりました。この日のために、必死に応用力に磨きをかけてきた人にとっては、物足りなさすら感じたと思います。
「難しい裁量問題を加えた」のではなく、「簡単な標準問題を加えた」と言わんばかりの作りで、裁量問題のあり方が問われると思っています。来年以降は間違いなく難化するはずで、そうでなければ、北海道の学力レベルが疑問視される事態となるでしょう…。
出題と難易度
難易度は★の数であらわしています。
【★★★★ 難しい│50点以上を目指す人】
【★★★☆ やや難しい│40点以上を目指す人】
【★★☆☆ 標準│30点以上を目指す人
【★☆☆☆ 易しい│20点以上を目指す人】
※今年は易しい出題であったため、◯点以上はあくまでも目安
| 大問No. | 小問No. | 配点 (60点満点) |
出題内容 | 難易度 | コメント |
| 大問1 | 問1 | 3点 | 因数分解 | ★☆☆☆ | すべてが基本。 |
| 問2 | 3点 | 作図 | ★☆☆☆ | ||
| 問3 | 4点 | 確率 | ★☆☆☆ | ||
| 問4 | 4点 | 円柱の体積 | ★☆☆☆ | ||
| 大問2 | 問1 | 3点 | 魔法陣の計算 | ★★☆☆ | 少し新傾向だが、落ち着いて図で理解できれば、立式は素直。 |
| 問2 | 4点 | 魔法陣の計算:連立の立式 | ★★★☆ | ||
| 大問3 | 問1 | 3点 | 二次関数:座標を求める | ★☆☆☆ | この2問は、ほぼ同じ解き方で答えられる。出題の幅がせまく易しい。 |
| 問2 | 3点 | 二次関数:2点を通る直線の傾き | ★★☆☆ | ||
| 問3 | 4点 | 二次関数:文字を使って立式 | ★★★★ | 山場のため★4にしたが、典型的な出題パターンのため解きやすい。 | |
| 大問4 | 問1 | 3点 | 台形と角度 | ★☆☆☆ | 図に書けば解ける。 |
| 問2 | 5点 | 三角形の合同を証明 | ★★★☆ | 証明の典型パターン、ひねりがなく解きやすい。 | |
| 大問5 | 問1(1) | 3点 | 1次関数と三平方の定理 | ★★☆☆ | 関数+三平方だが、基本の出題。 |
| 問1(2) | 4点 | 1次関数と相似 | ★★★★ | 山場なので★4にしたが、解く手順はシンプルで、融合問題にしては易しい。 | |
| 問2(1) | 3点 | 平均値 | ★☆☆☆ | 基本。 | |
| 問2(2) | 4点 | 階級値と度数から立式 | ★★★☆ | 階級値・度数+方程式の融合だが、表のまま式は立てやすい。 | |
| 問2(3) | 6点 | 階級値と度数を説明 | ★★★☆ | 発想があればひねりがなく、文章も素直に書きやすい。 |
解説編
大問1
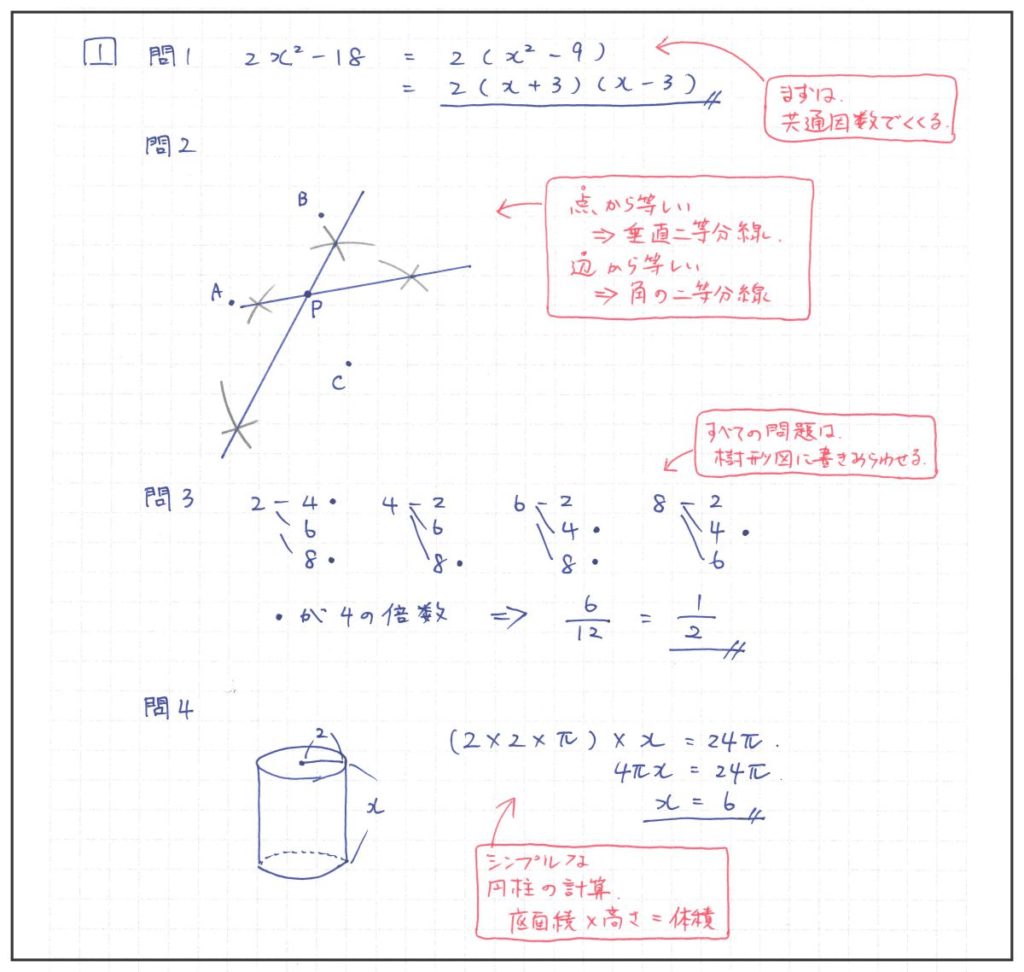
問1 因数分解
いきなり乗法公式に当てはまるのではなく、「共通因数でくくる」のが最初の手順です。
複雑な因数分解の定番パターンですので、お忘れなく。
問2 作図
垂直二等分線を使う、基本的な問題でした。
”点”から等しい場合は、垂直二等分線を使う。”辺”から等しい場合は、角の二等分線を使う。
この使い分けが難しい作図になっても活きてきますので、覚えておいてください。
問3 確率
「袋の中にもどさない」ので、1個目と2個目の区別がつく点に注意して、樹形図を書きます。
もし「袋の中にもどす」という問題であれば、1個目と2個目の重複を避けるため、樹形図が変わります。
問題によって見分けられるように練習しておきましょう。
問4 円柱の体積
【底面積×高さ】という、体積の求め方の基本だけおさえておけば解ける問題です。
大問2
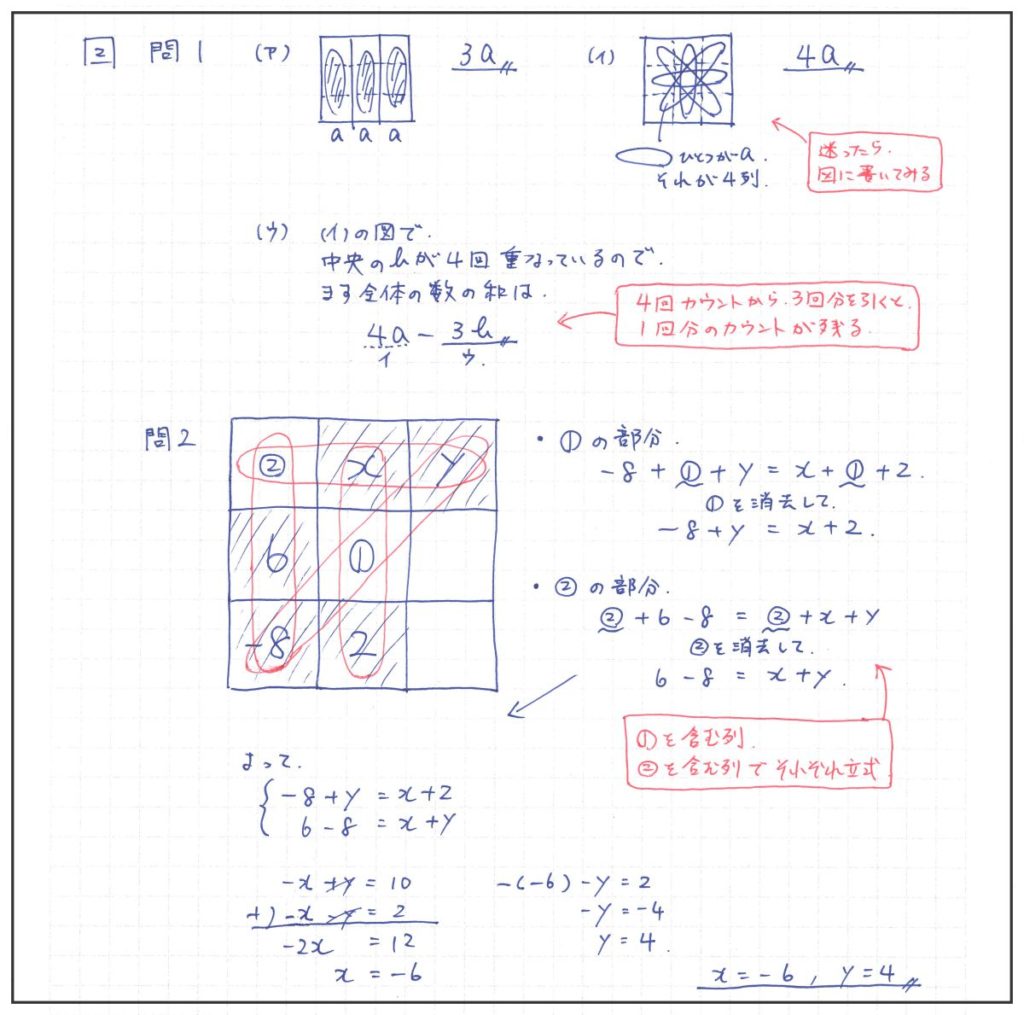
問1 魔法陣の計算:式の説明
(イ)の4列の和でbが4つ重なっているので、(ウ)の部分で-3bとすることで、余計な3回分を引くところがポイント。
こういう数の規則性に類する問題は、図に書きあらわすことが大事。可視化して、目で見て考える。
問2 魔法陣の計算:連立の立式
下記の解法例のように、2つの空白部分に対して、それぞれ2本ずつ式ができる。
このような新傾向の問題の場合、決まった解法パターンはない。いきなりキレイな方程式は出来なくても、やはり図に書きあらわし、手を動かして不完全でも式に書きあらわしてみることが大切。
仮に空白の部分を(1),(2)やa,bのように文字に置いてみると、そこが消去されて連立方程式が立てられる。
大問3
問1 二次関数:座標を求める
単純に、与えられた(2)の式にx=2を代入すれば、座標が求められる。
問2 二次関数:2点を通る直線の傾き
問1とほぼ同じで、代入ずればB,Cの座標はすぐ求められる。
あとはy=ax+bに座標を代入し、連立方程式でフィニッシュ。
求めるのが「傾き」である点が微妙にひっかけ。式を求めて答えてしまうと、アウト。
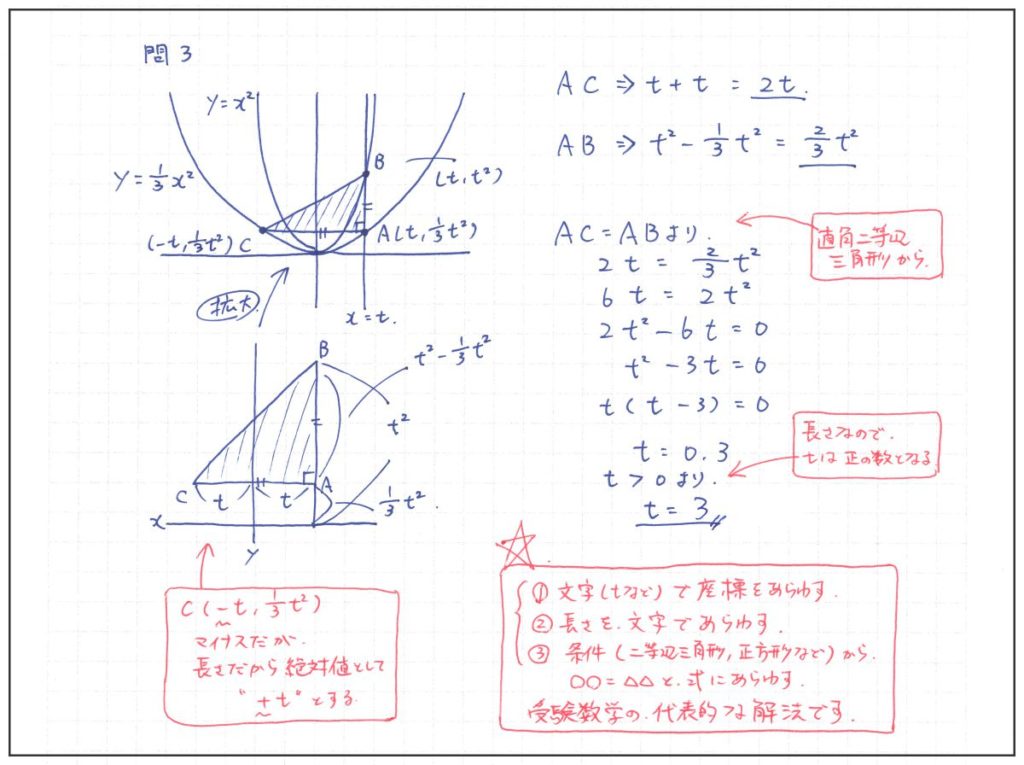
問3 二次関数:文字を使って立式
関数の山場の問題にあたるが、ひねりがなく、セオリー通りの解法で解ける。
(手順1)座標を文字tを使ってあらわす
(手順2)長さを文字tを使ってあらわす
(手順3)長さを条件にあてはめて式を立てる
この文字を使った【座標→長さ→立式】の手順は王道中の王道。ぜひともマスターしよう。

大問4
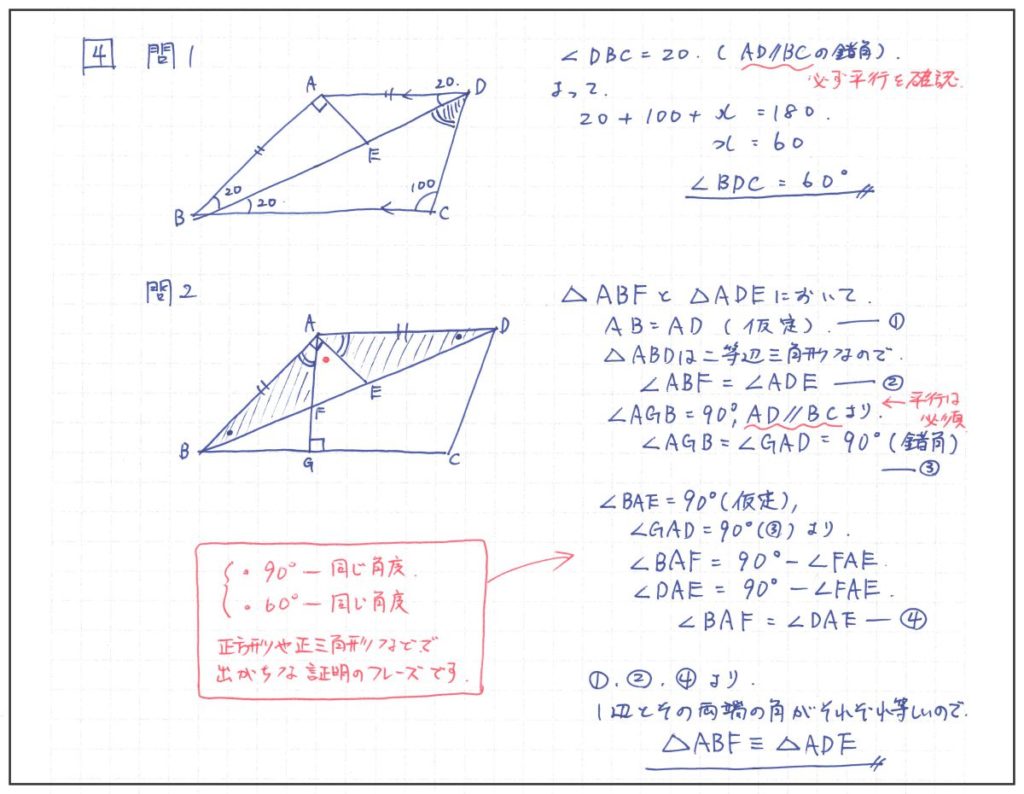
問1 台形と角度
平行と錯覚を利用すれば、簡単に求められる。
一発で解けなくても、とにかく図にわかる角度を書きこんでいけば、正答に近づくはず。
問2 三角形の合同を証明
難易度は中くらいだが、学校のワークにも必ず載っているくらい、よく見る問題パターン。
「∠A=90°-同じ角度、∠B=90°-同じ角度」とあらわすことから、∠A=∠Bと求めていく。
正三角形や正方形、垂直と相性が良い解法なので、その条件が出たら「しめしめ。」と思えると上出来。
大問5(裁量問題)
問1(1)1次関数と三平方の定理
あたえられた式にy座標を代入し点Aを求め、三平方の定理にもっていくだけ。一応、融合問題に類するが、解き方は簡単でシンプル。
問1(2)1次関数と相似
相似な図形を発見し、相似比を利用して長さを求める。その長さから、Cの座標を求める。
Cの座標がわかれば、y=axに代入してフィニッシュ。
【相似→1次関数→比例】とつながるが複雑さはなく、1つずつ手順を追えば答えが求められる、融合問題の基本のような出題。
問2(1)平均値
特にナシ。
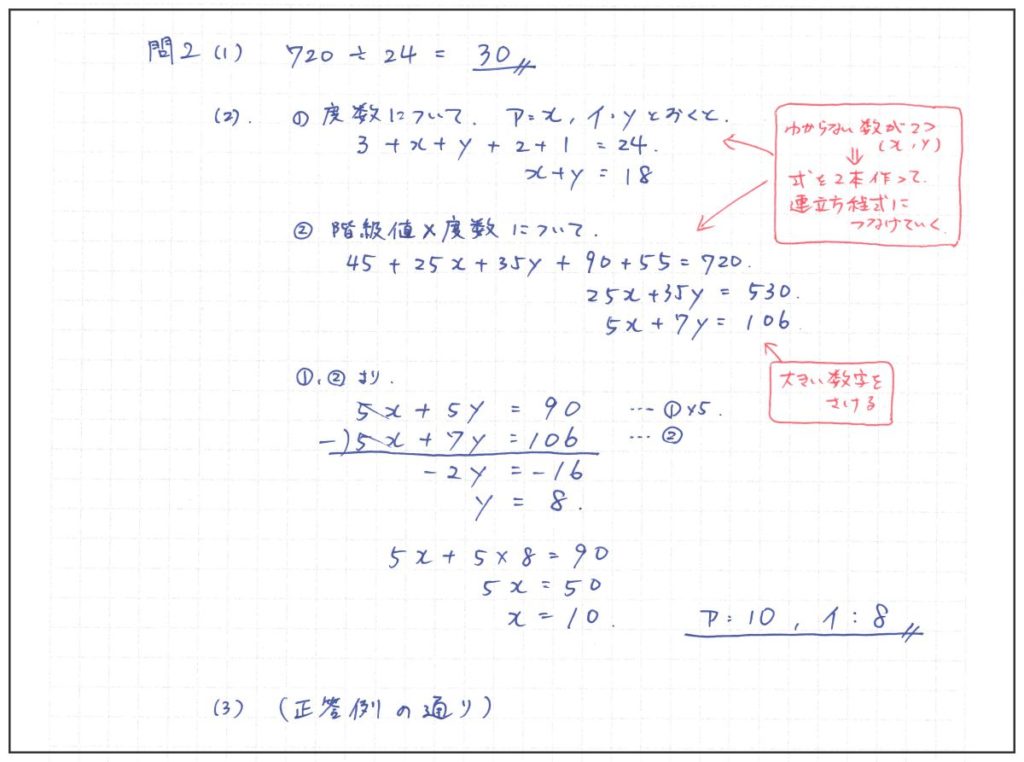
問2(2)階級値と度数から立式
階級値・度数を連立方程式の立式につなげる、融合問題。
よくみる形ではないが、表の空欄ア,イの部分をx,yと置いて、度数と階級値×度数でそれぞれ合計値を式にあらわせば、式が2本立てられる。
問2(3)階級値と度数を説明
条件に合わせて、階級値と度数について文章で説明する。
とっかかりのつかみにくさはあるが、発想さえ浮かべば文章に書くこと自体はそこまで難しくない。
中1「資料の活用」に関しては出題のパターンが多くないので、代表的な問題をおさえておけばOK。

以上です。
来年の受験生の参考になれば幸いです。
内容の訂正・質問・「こんな問題も解説してほしい」など要望がありましたら、コメントやメールフォームからお願いいたします!



