2018年9月19日(水)に各中学校で実施された、
学力テストA、数学の解説になります。
※当初は2018年9月13日(木)の実施予定でしたが、地震の影響により延期されました
詳しい解説については、計算問題など基本的なものは割愛させていただき、大問4の問3以降を掲載します。リクエストなどありましたら、問合せフォームよりお知らせください。
それでは、内容に進みます。
出題内容について
問題と難易度
| 大問 | 小問 | 出題 | 配点 | 難易度 | 内容について |
| 1 | 問1 | (1)正負の数の計算 | 2点 | ★☆☆☆ | -(-7)の符号に注意 |
| (2)文字の計算 | 2点 | ★☆☆☆ | ÷(-ab/2)の処理に注意 | ||
| (3)平方根の計算 | 2点 | ★☆☆☆ | √のカッコの外し方に注意 | ||
| 問2 | 因数分解 | 3点 | ★☆☆☆ | (a+3)をAと置き換え計算する | |
| 問3 | 方程式の利用 | 3点 | ★☆☆☆ | 1次方程式にx=-5を代入し、aの値を求める | |
| 問4 | 2次方程式を解く | 3点 | ★☆☆☆ | 分数が混じった2次方程式を解く | |
| 問5 | 平行四辺形と角度 | 3点 | ★☆☆☆ | 平行四辺形と二等辺三角形の性質を利用する | |
| 2 | 問1 | 比例式/値を求める | 3点 | ★☆☆☆ | ( )の処理に注意 |
| 問2 | 1次関数の交点 | 3点 | ★☆☆☆ | 2直線の式を求める →連立方程式で交点の座標を求める |
|
| 3 | 問1 | 度数分布表 | 3点 | ★☆☆☆ | 記号で4択の問題 最頻値・相対度数・中央値の用語が出てくる |
| 問2 | 相対度数を求める | 3点 | ★☆☆☆ | 中央値がふくまれている階級の相対度数を求める | |
| 4 | 問1 | 平方根+展開の計算 | 3点 | ★★☆☆ | 乗法公式を利用して計算 |
| 問2 | 2次方程式を解く | 3点 | ★★☆☆ | 展開から式をまとめる、あとは解くだけ | |
| 問3 | 連立方程式の文章題 (速さ) |
4点 | ★★☆☆ | オーソドックスな出題、一切ひねりなし | |
| 問4 | 1次関数/変域の利用 | 4点 | ★★☆☆ | xとyの変域を組み合わせる →代入する座標がわかり、計算が進む |
|
| 5 | 作図 | 4点 | ★★★☆ | 使うのは垂線のみだが、発想が必要 | |
| 6 | 問1 | 1次関数+図形の移動 /式を求める |
4点 | ★★★☆ | 図形の重なり方で式が異なる →図から入り、場合分けをしていく |
| 問2 | /ある面積のときのxの値 | 4点 | ★★★★ | 問1よりも場合分けの判断が難しい →正しい答えを選ぶ必要がある |
|
| 7 | 合同の証明 (正方形の回転移動) |
4点 | ★★★★ | 図から正三角形を探し出せると証明が進む →与えられた過程を適切に使う必要アリ |
講評
【★☆☆☆】まで全問正解:30点
【★★☆☆】まで全問正解:44点
【★★★☆】まで全問正解:52点
【★★★★】まで全問正解:60点
易しめの作りで、基礎問題だけで優に40点は超えられる出題でした。裁量問題を採択している学校を受験する人は、40点前後は得点したいところです。
★×1や★×2で失点が多い人は、難しい問題に進まず基礎レベルの問題を繰り返し勉強した方が良いと思います。
大問5以降には★×3や★×4をつけましたが、裁量問題に比べると易しい問題といえます。
大問5の作図や大問7の図形問題は、やや発想が浮かびにくいですが、取っかかりさえつかめれば手が進むはずです。大問6は場合分けが厄介でしたが、図を書き出して状況が把握できれば、計算自体は難しくありません。東西南北を目指す人は、これらの問題も解けるようになり、50点以上を狙いたいところです。
大問4 問3 連立利用/問4 関数と変域
問3 連立方程式の文章題(速さ)
文章題ではあるものの、オーソドックスな出題でした。
一般的なレベルの問題集には、必ず収録されているような問題です。
基本だからこそ、
・図に書いて「距離/時間/速さ」を書きあらわす
・加減法/代入法を判断して計算する
・大きい数字を割ってから計算する
などといった、連立方程式の解き方を確実におさえてください。
問4 1次関数と変域の利用
数字だけ追うとイメージがわきにくいので、下の解説のように、グラフに書き出してから解きます。
グラフは解法のヒントです。「計算の手が動かない」「発想が浮かばない」という人は、日頃から書き出す練習をしておきましょう。
この問題の場合は、グラフに書き出すと( -3 , 11 )と片方の座標が読み取れます。代入すると直線の式がわかり、それにもう片方の座標を代入して終了です。

大問6 1次関数と図形の利用
問1 ある変域のときの式を求める
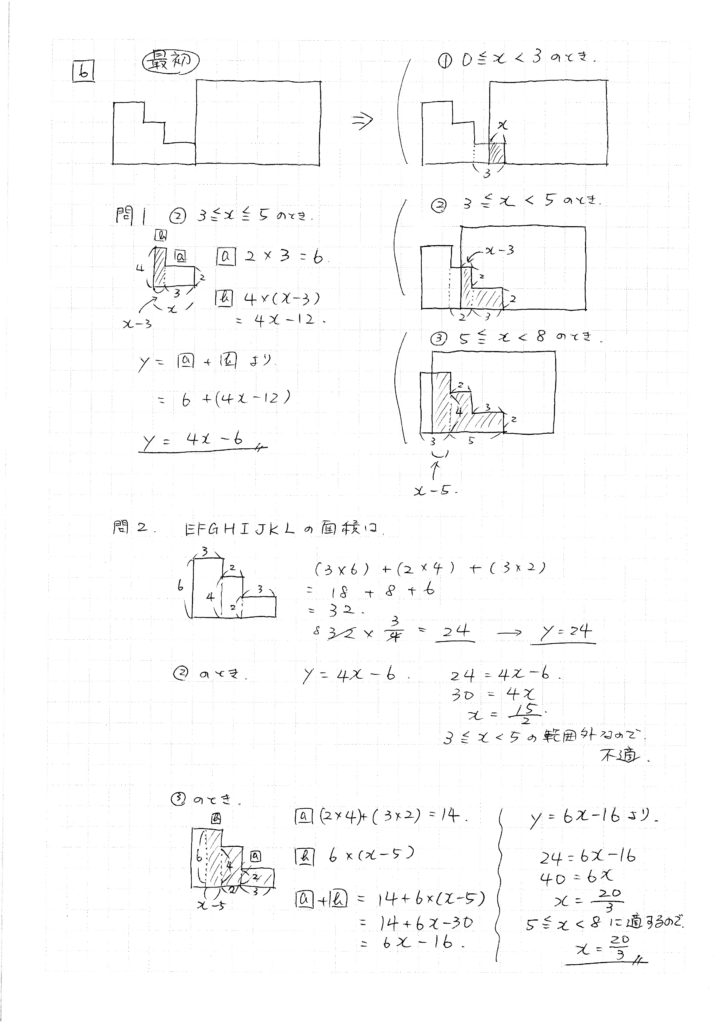
下記の解法の(1)(2)(3)のように、場合分けが必須です。
階段のような変わった図形が移動しますが、それぞれの状況に合わせて図を書き、長さも書き入れます。変域から図を書き分けても良いですし、イメージを図に書きあらわしてから変域を考えても良いですし、それはやりやすい方で構いません。とにかく図を書くことに慣れてください。
問題で指示された「3≦x≦5」の変域の図を書けたら、あとは長さをあらわし、面積を計算していくだけです。
問2 ある面積のときのxの値を求める
問題で指示された「EFGHIJKLの面積の3/4 → y=24」が、どの変域の場合なのかを見極めなければなりません。
下記の解法では3つの変域に分けて場合分けしているのですが、解法では(2)(3)の2つを計算しています。
(2)の場合、計算した結果「x=15/2」と求められるのですが、これは「3≦x≦5」という変域外の値なので、答えとして不適になります。このように場合分けが必要な問題は、「条件に適した答えを選ぶ」という手間がかかりますので、答えを出した勢いのまま終了することがないように、気をつけてください。
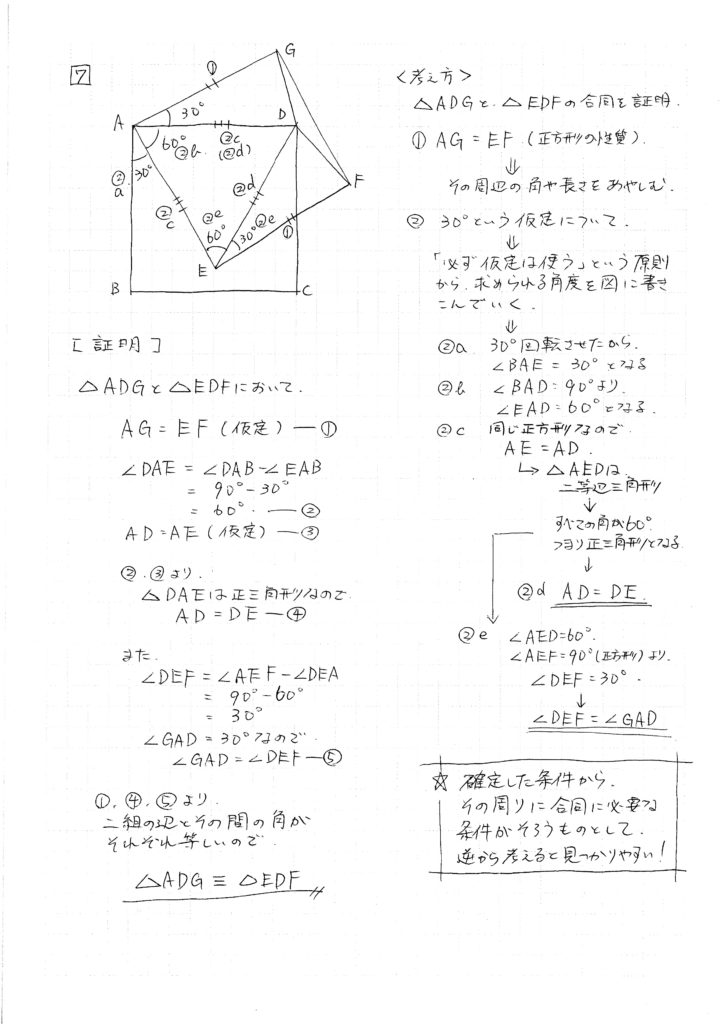
大問7 合同/正方形と二等辺三角形
どこを手がかりに合同を証明したら良いのか「わかりそうでわからない」という人が多そうな問題です。
「与えられた仮定は必ず使う」というのが証明問題のセオリーです。
この問題の場合、2つの正方形が書かれているので、「正方形 = すべての辺と角が等しい」という条件を書きこみます。さらに「反時計回りに30°回転移動」しているのですから、その角度も書きこみます。
これらから△ADEが正三角形となることを導き出せれば、証明が進められるはずです。
以上です。
また学力Bテストなども更新いたします。



